Correlation Clustering with a Fixed Number of Clusters
by Ioannis Giotis and Venkatesan Guruswami
Theory of Computing, Volume 2(13), pp. 249-266, 2006
Bibliography with links to cited articles
[1] A. Agarwal, M. Charikar, K. Makarychev, and Y. Makarychev:
O(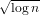 ) approximation algorithms for Min Uncut, Min 2CNF deletion,
and directed cut problems. In Proc. 37th STOC, pp. 573–581. ACM Press,
2005. [STOC:10.1145/1060590.1060675].
) approximation algorithms for Min Uncut, Min 2CNF deletion,
and directed cut problems. In Proc. 37th STOC, pp. 573–581. ACM Press,
2005. [STOC:10.1145/1060590.1060675].
[2] N. Ailon, M. Charikar, and A. Newman: Aggregating Inconsistent Information: Ranking and Clustering. In Proc. 37th STOC, pp. 684–693. ACM Press, 2005. [STOC:1060590.1060692].
[3] N. Alon, K. Makarychev, Y. Makarychev, and A. Naor: Quadratic forms on graphs. In Proc. 37th STOC, pp. 486–493. ACM Press, 2005. [STOC:10.1145/1060590.1060664].
[4] S. Arora, E. Berger, E. Hazan, G. Kindler, and S. Safra: On non-approximability for quadratic programs. In Proc. 46th FOCS, pp. 206–215. IEEE Computer Society Press, 2005. [FOCS:10.1109/SFCS.2005.57].
[5] N. Bansal, A. Blum, and S. Chawla: Correlation clustering. Machine Learning, Special Issue on Clustering, 56:89–113, 2004. [doi:10.1023/B:MACH.0000033116.57574.95].
[6] A. Ben-Dor, R. Shamir, and Z. Yakhini: Clustering gene expression patterns. Journal of Computational Biology, 6:281–297, 1999.
[7] M. Charikar, V. Guruswami, and A. Wirth: Clustering with qualitative information. Journal of Computer and System Sciences, 71(3):360–383, October 2005. [JCSS:10.1016/j.jcss.2004.10.012].
[8] M. Charikar and A. Wirth: Maximizing quadratic programs: extending Grothendieck’s inequality. In Proc. 45th FOCS, pp. 54–60. IEEE Computer Society Press, 2004. [FOCS:10.1109/FOCS.2004.39].
[9] E. Demaine and N. Immorlica: Correlation clustering with partial information. In Proc. 6th Internat. Workshop on Approximation Algorithms for Combinatorial Optimization Problems (APPROX’03), volume 2764 of LNCS, pp. 1–13. Springer, 2003. [doi:10.1007/b11961].
[10] D. Emanuel and A. Fiat: Correlation clustering—minimizing disagreements on arbitrary weighted graphs. In Proc. 11th European Symp. on Algorithms (ESA’03), pp. 208–220. Springer, 2003. [doi:10.1007/b13632].
[11] W. Fernandez de la Vega, M. Karpinski, C. Kenyon, and Y. Rabani: Approximation schemes for clustering problems. In Proc. 35th STOC, pp. 50–58. ACM Press, 2003. [STOC:10.1145/780542.780550].
[12] W. Fernandez de la Vega and C. Kenyon: A randomized approximation scheme for metric max-cut. In Proc. 39th FOCS, pp. 468–471. IEEE Computer Society Press, 1998. [FOCS:10.1109/SFCS.1998.743497].
[13] O. Goldreich, S. Goldwasser, and D. Ron: Property testing and its connection to learning and approximation. Journal of the ACM, 45(4):653–750, July 1998. [JACM:10.1145/285055.285060].
[14] P. Indyk: A sublinear-time approximation scheme for clustering in metric spaces. In Proc. 40th FOCS, pp. 154–159. IEEE Computer Society Press, 1999. [FOCS:10.1109/SFFCS.1999.814587].
[15] S. Khot, G. Kindler, E. Mossel, and R. O’Donnell: Optimal inapproximability results for Max Cut and other 2-variable CSPs. In Proc. 45th FOCS, pp. 146–154. IEEE Computer Society Press, 2004. [FOCS:10.1109/FOCS.2004.49].
[16] A. Nemirovski, C. Roos, and T. Terlaky: On maximization of quadratic form over intersection of ellipsoids with common center. Mathematical Programming, 86(3):463–473, 1999. [STACS:922f1ftd6bpfxhk7].
[17] R. Shamir, R. Sharan, and D. Tsur: Cluster graph modification problems. In Proc. 28th Workshop on Graph Theory (WG’02), pp. 379–390, 2002.
[18] C. Swamy: Correlation Clustering: Maximizing agreements via semidefinite programming. In Proc. 15th ACM-SIAM Symp. on Discrete Algorithms (SODA’04), pp. 519–520. SIAM, 2004. [SODA:982866].
